Công thức tính động năng

Các bạn thân mến, công thức tính động năng chúng ta đã từng được giới thiệu qua trong chương trình học từ THCS, THPT. Hôm nay chúng ta cùng ôn lại công thức này cũng như các vấn đề liên quan đến động năng các bạn nhé

Giới thiệu về động năng

Động năng là gì?

Theo định nghĩa của động năng, khi một vật di chuyển, nó sẽ mang theo một lượng năng lượng. Động năng của một vật được tính toán dựa trên khối lượng và vận tốc của vật đó. Hiểu đơn giản hơn động năng của một vật có được do quá trình chuyển động của vật đó. Chính vì vật mang động năng nên nó có thể tác động lực lên các vật khác và lực này sẽ sinh công

Ý nghĩa của động năng trong cuộc sống và khoa học kỹ thuật

Tầm quan trọng của động năng là rất lớn trong vật lý. Nó được sử dụng trong nhiều lĩnh vực, bao gồm cả cơ học, điện học, nhiệt học và vật lý hạt nhân. Động năng là một trong những khái niệm cơ bản để giải thích các hiện tượng vật lý, từ các chuyển động đơn giản đến các hiện tượng phức tạp như sự phát xạ của hạt nhân. Việc tính toán dựa vào công thức tính động năng cho ra con số cụ thể giúp việc nghiên cứu các vấn đề trên được giải quyết chính xác và dễ dàng

Ngoài ra,việc sử dụng công thức tính động năng còn được sử dụng để giải quyết các vấn đề thực tiễn, như tính toán động cơ, phân tích các vấn đề liên quan đến môi trường, thiết kế các kết cấu vật lý, và cải thiện hiệu quả năng lượng. Do đó, hiểu về động năng là rất quan trọng trong việc học và nghiên cứu vật lý.

Lịch sử của động năng và công thức tính động năng

Khái niệm về động năng được hình thành và phát triển qua nhiều giai đoạn lịch sử khác nhau. Dưới đây là những giai đoạn quan trọng trong lịch sử hình thành và phát triển của động năng:

1. Giai đoạn cổ đại:

• Các nhà triết học Hy Lạp đã nghĩ đến khái niệm về động năng như Tha-lê, A-ri-stô, và Eu-ri-phê-nê, nhưng ý tưởng này chưa được phát triển rõ ràng và đầy đủ.

2. Giai đoạn trung cổ:

• Trong thời kỳ này, các nhà triết học Hồi giáo như Avicenna và Averroes đã đưa ra những ý tưởng về động năng và năng lượng, tuy nhiên đó mới chỉ là hình thành ý tưởng và công thức tính động năng lúc đó vẫn đang còn mơ hồ chưa cụ thể nhưng lại bị lãng quên sau đó.

3. Giai đoạn đầu thời kỳ phục hưng:

• Các nhà khoa học thời kỳ này như Leonardo da Vinci và Galileo Galilei đã đưa ra các quan điểm về động năng, nhưng chúng chưa được biểu diễn bằng các công thức tính động năng cụ thể.

4. Giai đoạn của Newton:

• Công trình “Principia Mathematica” của Isaac Newton, được xuất bản vào năm 1687, đã đưa ra công thức tính động năng chính xác để tính động năng của một vật di chuyển. Đây được coi là bước đột phá lớn trong lịch sử hình thành và phát triển của động năng.

5. Giai đoạn phát triển đầy đủ của động năng:

• Trong thế kỷ 19, các nhà vật lý như James Prescott Joule, Hermann von Helmholtz và Julius von Mayer đã đưa ra những ý tưởng mới về động năng và năng lượng, đóng góp rất lớn vào việc phát triển và mở rộng khái niệm về động năng.

6. Giai đoạn đương đại:

• Hiện nay, động năng được sử dụng rộng rãi trong các lĩnh vực khác nhau của khoa học và công nghệ. Các công nghệ mới như điện tử, năng lượng tái tạo và công nghệ xây dựng đều dựa trên khái niệm về động năng và năng lượng, giúp con người có thể nghiên cứu và áp dụng nó vào thực tiễn một cách hiệu quả hơn. Nhờ có công thức tính động năng, việc nghiên cứu, ứng dụng trong các lĩnh vực khoa học kỹ thuật đơn giản hơn rất nhiều.

Công thức tính động năng

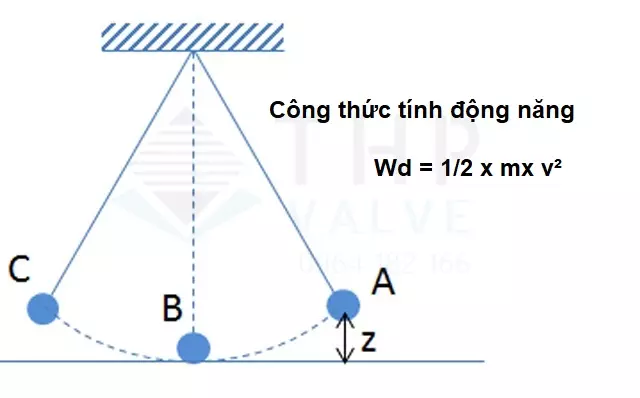
Công thức tính động năng

Động năng được tính toán theo công thức:

Wd = 1/2mv²

Trong đó:

Wd: Là động năng(Đơn vị là Jun- Viết tắt là J)

m: Khối lượng của vật(Đơn vị là ki lô gam – Viết tắt là kg)

v: Vận tốc của vật(Đơn vị là mét/giây – Viết tắt là m/s)

Công thức trên cho phép tính toán lượng động năng mà vật đang có khi di chuyển với một vận tốc nhất định. Nói cách khác, công thức tính động năng cho phép chúng ta biết được khả năng làm việc hoặc sản xuất lượng công suất mà vật có thể tạo ra dựa trên vận tốc và khối lượng của nó.

Nếu vật không di chuyển thì động năng của nó bằng 0. Nếu vật di chuyển đều thì động năng của nó là hằng số. Nếu vật di chuyển theo quỹ đạo cong hoặc không đều thì động năng của nó có thể thay đổi theo thời gian và vị trí của nó.

Công thức tính động năng là một trong những công thức cơ bản nhất trong vật lý và được sử dụng rộng rãi trong các lĩnh vực như cơ khí, điện tử, năng lượng, và khoa học vật liệu.

Ngoài ra công thức tính động năng còn được áp dụng cho hệ thống gồm có nhiều vật mà các vật đó không tác động lẫn nhau và không bị mất mát năng lượng.

Wd = 1/2 x ∑(m x v²)

Ví dụ:

Giả sử bạn có một hệ thống gồm hai vật, vật A có khối lượng 2 kg và đang di chuyển với vận tốc 3 m/s, vật B có khối lượng 3 kg và đang di chuyển với vận tốc 2 m/s. Hãy tính động năng của toàn bộ hệ thống.

Áp dụng công thức tổng quát, ta có:Wd= 1/2 * Σ(m * v²)

Thay số vào Wd = 1/2 * [(2 kg * (3 m/s)²) + (3 kg * (2 m/s)²)] K = 19,5 J

Vậy, động năng của toàn bộ hệ thống là 19,5 Jun

Ví dụ minh họa về công thức tính động năng

Ví dụ 1: Giả sử bạn có một vật có khối lượng là 2 kg đang chuyển động với vận tốc là 6 m/s. Hãy tính động năng của vật đó?

Áp dụng công thức: Wd  =  1/2 mv²

Thay số vào chúng ta được: 1/2 x 2 x 6² = 36(J)

Như vậy chúng ta tính được động năng của vật là 36 Jun

Ví dụ 2: Bạn đạp xe đạp thể dục với tổng trọng lượng là 70kg, vận tốc di chuyển là 15m/s

Vậy Ta có thể tính toán động năng của người và xe đạp bằng công thức tính động năng:

Wd = 1/2mv² = 1/2 x 70 x 15² = 7.875 (J)

Như vậy động năng của người và xe đạp là 7875 Jun. Điều này có thể được áp dụng để tính toán lượng năng lượng mà người này tiêu thụ khi đi xe đạp và tính toán lượng năng lượng cần thiết để di chuyển của cả người và xe

Ứng dụng của công thức tính động năng

Việc nghiên cứu và tìm ra được công thức tính động năng đã giúp chúng ta phân tích, đưa ra các con số cụ thể cho nhiều trường hợp cần tính toán từ đơn giản đến phức tạp. Từ đó có được những con số chính xác để áp dụng vào cuộc sống và sản xuất

• Tính toán năng lượng cần thiết để vật di chuyển từ một vị trí này đến một vị trí khác, ví dụ như khi tính năng lượng cần thiết để đưa một vật từ bãi đỗ xe lên đến đỉnh của một đồi.
• Tính toán công suất cần thiết của một động cơ để nâng một vật nặng lên cao bằng việc sử dụng công thức tính động năng, công suất cần thiết để nâng một vật sẽ phụ thuộc vào khối lượng của vật và độ cao cần nâng lên. Từ đó đưa ra các phương án khả thi đặc biệt trong lĩnh vực kiến trúc, xây dựng
• Tính toán năng lượng cần thiết để tăng tốc một vật đến một vận tốc nhất định. Ví dụ, trong thiết kế và tính toán các máy bay hoặc tàu hỏa, công thức động năng được sử dụng để tính toán năng lượng cần thiết để tăng tốc một phương tiện từ tốc độ ban đầu đến tốc độ cuối cùng.
• Công thức tính động năng cũng được sử dụng trong lĩnh vực năng lượng tái tạo, để tính toán năng lượng mà một hệ thống điện mặt trời hoặc hệ thống gió có thể tạo ra.
• Trong công nghiệp, công thức động năng được sử dụng để tính toán năng lượng cần thiết để vật di chuyển hoặc vật quay trong các hệ thống máy móc, lực kéo của các động cơ sinh công dùng cho công nghiệp(Các loại mô tơ, van điều khiển điện, van điều khiển khí nén…)
• Ứng dụng trong lĩnh vực hàng không vũ trụ: Tính toán để đưa ra các lực đẩy của động cơ phản lực, tên lửa đẩy giúp nâng cao khả năng vận chuyển, chinh phục vũ trụ bao la
• Trong công nghệ hóa học, công thức động năng được sử dụng để tính toán năng lượng cần thiết để phân tích các chất phức tạp và phản ứng hóa học, để giải quyết các vấn đề liên quan đến tổng hợp và sản xuất.
• Công thức động năng được sử dụng trong tính toán động lực học của các phản ứng hạt nhân, chẳng hạn như phản ứng hạt nhân trong vũ trụ và trong các đại học nghiên cứu hạt nhân. Nó cũng được áp dụng nhiều trong các nghiên cứu hóa học để tính phản ứng của các nguyên tố, từ đó đưa ra được các phân tích chuyên sâu hơn nữa về ngành hóa học này

Đánh giá về công thức tính động năng

Điểm mạnh và điểm yếu của công thức tính động năng

Công thức động năng là một công thức rất quan trọng trong vật lý và được sử dụng rộng rãi trong nhiều ngành khoa học và công nghiệp. Nó cho phép tính toán năng lượng của một vật di chuyển, dựa trên khối lượng và vận tốc của nó.

Một trong những ưu điểm lớn của công thức động năng là tính toán đơn giản và dễ dàng sử dụng. Nó chỉ yêu cầu hai thông số cơ bản là khối lượng và vận tốc của vật, giúp tiết kiệm thời gian và công sức cho những tính toán phức tạp hơn.

Ngoài ra, công thức động năng còn có tính chất bảo toàn năng lượng, tức là tổng năng lượng của hệ thống không bị thay đổi trong quá trình chuyển đổi từ năng lượng động sang năng lượng tiềm năng và ngược lại. Điều này giúp cho việc tính toán và đánh giá các hiện tượng liên quan đến năng lượng trở nên dễ dàng hơn.

Tuy nhiên, cũng cần lưu ý rằng công thức động năng chỉ có thể áp dụng đúng cho các hệ thống vật chất tuyến tính và chuyển động thẳng đều. Đối với các hệ thống vật chất không tuyến tính và chuyển động không đều, công thức này có thể không cho kết quả chính xác.

Có thể kết luận rằng, công thức động năng là một công cụ quan trọng và hữu ích trong nhiều ngành khoa học và công nghiệp. Tuy nhiên, để sử dụng công thức này hiệu quả, cần phải hiểu rõ giới hạn của nó và áp dụng đúng cách vào từng trường hợp cụ thể. Có như vậy chúng ta mới có được thông số chính xác nhất phục vụ cho mục đích sử dụng

Cách sử dụng công thức tính động năng hiệu quả

Để sử dụng công thức động năng hiệu quả, có thể làm theo các bước sau:

1. Xác định các thông số cần thiết: Khối lượng và vận tốc của vật. Các thông số này phải được đo đạt chính xác và được chuyển về đơn vị tiêu chuẩn để tính toán.
2. Tính toán động năng: Sau khi có các thông số cần thiết, sử dụng công thức động năng để tính toán năng lượng của vật di chuyển.
3. Kiểm tra và đánh giá kết quả: Đối chiếu kết quả tính toán với các giá trị thực tế để đảm bảo tính chính xác của kết quả. Nếu có sai số, cần kiểm tra lại các thông số đầu vào và cách tính toán để tìm ra nguyên nhân và khắc phục.
4. Áp dụng kết quả: Dựa trên kết quả tính toán động năng, có thể áp dụng vào các bài toán liên quan đến năng lượng, như tính toán công suất, độ hiệu quả của các hệ thống máy móc, hay tính toán các động cơ và máy móc khác.

Ngoài ra, để sử dụng công thức tính động năng hiệu quả, cần phải hiểu rõ giới hạn của công thức và áp dụng đúng cách vào từng trường hợp cụ thể. Nếu hệ thống vật chất không tuyến tính hoặc chuyển động không đều, công thức này có thể không cho kết quả chính xác và cần phải áp dụng các công thức khác phù hợp hơn.

Kết luận: Trên đây là toàn bộ bài viết của chúng tôi về chủ đề công thức tính động năng. Động năng là một khái niệm quan trọng trong vật lý. Nhờ việc nghiên cứu ra động năng cũng như công thức tính giúp chúng ta có thể áp dụng và tính toán chính xác các hiện tượng, sự vật, vật chất xung quanh đưa ra con số tính toán chính xác và hiệu quả để phục vụ sản xuất, khoa học kỹ thuật

Chúng tôi đã giới thiệu cho bạn đọc về khái niệm, lịch sử hình thành và phát triển của động năng cũng như ứng dụng của động năng và công thức tính động năng vào cuộc sống và công nghiệp

Cảm ơn các bạn đã quan tâm và theo dõi bài viết, hẹn gặp lại ở các bài viết sau về các kiến thức trong ngành công nghiệp. Mong nhận được phản hồi và cùng thảo luận các nội dung với bạn đọc sâu hơn nữa